Оналайн-олимпиада Фоксфорд-2022
1 уровень (Базовый)
7-8 класс
Задача 1. Коробки с дронами.
На прилавке магазина стоят 9 коробок с разным количеством дронов внутри. Числа в таблице означают вместимость каждой коробки.
| 7 | 8 | 9 | 4 | 5 | 6 | 1 | 2 | 3 |
Продавец захотел переставить их для своего удобства, решил что будет переставлять в обратном порядке (первая встает на место последней, вторая - предпоследней и т.д) и выполнил следующие действия:
1. Переставил все девять коробок.
2. Переставил коробки с тремя, двумя и одним дроном.
3. Переставил коробки с шестью, пятью, четырьмя дронами.
4. Переставил коробки с девятью, восьмью и семью дронами.
В ответе укажите, сколько дронов лежит в крайней справа коробке.
Ответ: 9
В ответе укажите, сколько дронов лежит в крайней слева коробке.
Ответ: 1
Решение задачи:
Для удобства составим таблицу:
| Исходное состояние | 7 | 8 | 9 | 4 | 5 | 6 | 1 | 2 | 3 |
| Переставил все 9 коробок | 3 | 2 | 1 | 6 | 5 | 4 | 9 | 8 | 7 |
| Переставил третью, вторую и первую | 1 | 2 | 3 | 6 | 5 | 4 | 9 | 8 | 7 |
| Переставил шестую, пятую, четвёртую | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 8 | 7 |
| Переставил девятую, восьмую и седьмую | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Задача 2. Почистим память?
На пятнадцатилетие бабушка подарила Оле планшет с объёмом встроенной памяти 64 Гб.
На каникулах девочка решила оптимизировать свой гаджет, т.к. в последнее время он стал очень медленно работать. Программа для очистки памяти показала, что 21% памяти занимают файлы данных, 9% - бесполезные файлы, 17% - пакеты, 53% - память.
Определите, какой объём памяти в мегабайтах она освободит, удалив файлы данных и бесполезные файлы.
В качестве ответа укажите целую часть числа. Так, например, для ответа 40,9 в поле ввода нужно ввести 40.
Ответ: 19660
Решение задачи:
21 + 9 = 30% - объём памяти, который необходимо удалить.
0,3 * 64 = 19,2 Гб - объём удалённой памяти в гигабайтах.
19,2 * 1024 = 19 660,8 Мб
Задача 3. Алгоритмы и их свойства.
Петя и Ваня играли в игру. Сначала они написали на доске 6 троек и 6 четвёрок и договорились, что можно стереть две любые цифры. Если они будут одинаковыми, то нужно написать тройку, а если разными - четвёрку. Если в конце игры на доске останется число 4, то выиграет первый игрок, если 3, то второй. Кто победит в этой игре? Известно, что первый ход сделал Ваня.
В качестве ответа выберите имя мальчика:
- Петя
- Ваня
Ответ: Петя
Решение задачи:
Для каждого из участников игры возможны три варианта хода:
1) зачеркнуть две четвёрки;
2) зачеркнуть две тройки;
3) зачеркнуть одну четвёрку и одну тройку.
Ситуация на доске после каждого из возможных ходов:
| Вариант | Исчезнут цифры | Добавится цифра | Количество четвёрок | Количество троек |
| 1 | 44 | 3 | Уменьшится на 2 | Увеличится на 1 |
| 2 | 33 | 3 | Не изменится | Уменьшится на 1 |
| 3 | 43 | 4 | Не изменится | Уменьшится на 1 |
Из таблицы видно, что при любой последовательности ходов количество четвёрок останется чётным (и когда-то обязательно станет равным 0). Значит, на доске никогда не может остаться одна четвёрка, т.е. в этой игре всегда выиграет второй участник - Петя.
Задача 4. Кодирование, криптография.
Однажды холодным зимним вечером друг мистера Фокса получил письмо по электронной почте: «Дорогой друг, я решил отправиться в путешествие. Попробуй угадать название страны, в которую я улетел. В качестве подсказки высылаю три картинки. Если будешь внимательным, то быстро догадаешься, где я сейчас нахожусь. До скорой встречи!»

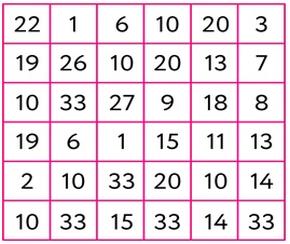

В ответе укажите название страны без пробелов и знаков препинания, в которой мистер Фокс проводит отпуск.
Ответ: Австралия
Решение задачи:
Двухцветная картинка - это трафарет, и если наложить её на квадрат с числами, мы получим порядковые номера букв в русском алфавите. Дальше стоит воспользоваться таблицей с буквами и заменить ими полученные числа.
Задача 5. Международная научная лунная станция.

Новый экипаж из 18 селенологов (астрономов, изучающих Луну) и 12 космобиологов прибыл на Международную научную лунную станцию (МНЛС). Этого количества специалистов хватает для обеспечения нормальной работы всей станции. В первую неделю после приезда экипажу необходимо выбрать командира и его заместителя. Известно, что во время выборов 2 селенолога и 4 космобиолога добровольно отказались от участия в выборах и не смогут занять эти должности. Сколькими способами можно назначить командира и его заместителя?
В ответе введите количество возможных вариантов.
Ответ: 552
Решение задачи:
Найдём общее количество людей, которые могут быть избраны на должности. Вычтем селенологов и космобиологов, отказавшихся от участия:
(18 - 2) + (12 - 4) = 16 + 8 = 24 человека. Командиром может стать любой из 24 членов экипажа. После выбора капитана на роль его заместителя могут претендовать 23 оставшихся человека. Таким образом, всего есть 24 * 23 = 552 разных варианта.
Задача 6. Джонни Пэп играет в «Майнкрафт».

Джонни Пэп решил поиграть в «Майнкрафт». Перед ним лежат 6 разных игровых предметов: три короткие плиты и три обычных блока. Короткие плиты: дубовая, еловая, берёзовая. Обычные блоки: железный, золотой, алмазный. Джонни Пэп построил секретный портал и расположил блоки в определённом порядке. Вот как он его описал:
- алмазный блок лежит с краю;
- ряд начинается не с обычного блока;
- золотой блок находится рядом с алмазным;
- берёзовая плита лежит между обычными блоками;
- еловая плита не с краю.
В каком порядке расположил игровые предметы Джонни Пэп?
Выберите для каждого порядкового номера соответствующий игровой предмет из списка.
Ответ: 1 - дубовая плита, 2 - еловая плита, 3 - железный блок, 4 - березовая плита, 5 - золотой блок, 6 - алмазный блок.
Решение задачи:
Алмазный блок находится с краю, но ряд начинается не с обычного блока, значит, этот блок стоит в самом конце. Рядом с алмазным блоком лежит золотой. Берёзовая плита лежит между обычными блоками, значит, она находится между железным и золотым. Еловая плита на втором месте, а на первом - дубовая плита.
Задача 6 (Вариант 2):
Джонни Пэп решил поиграть в «Майнкрафт». Перед ним лежат 6 разных игровых предметов: три короткие плиты и три обычных блока. Короткие плиты: дубовая, еловая, берёзовая. Обычные блоки: железный, золотой, алмазный. Джонни Пэп построил секретный портал и расположил блоки в определённом порядке. Вот как он его описал:
- алмазный блок лежит с краю;
- ряд заканчивается плитой;
- золотой блок находится рядом с алмазным;
- берёзовая плита лежит между обычными блоками;
- еловая плита не с краю.
В каком порядке расположил игровые предметы Джонни Пэп?
Выберите для каждого порядкового номера соответствующий игровой предмет из списка.
Ответ: 1 - алмазный блок, 2 - золотой блок, 3 - берёзовая плита, 4 - железный блок, 5 - еловая плита, 6 - дубовая плита .
Решение задачи:
Алмазный блок находится с краю, но ряд заканчивается плитой, значит, этот блок стоит в самом начале. Рядом с алмазным блоком лежит золотой. Берёзовая плита лежит между блоками, значит, она находится между железным и золотым. Еловая плита на предпоследнем месте, а на последнем - дубовая плита.
Задача 7. Экспедиция на Северный полюс.
8 путешественников готовятся к экспедиции на Северный полюс. Участников разделят на две группы, одна из которых будет проводить научные исследования на дрейфующей станции «Север-1», а другая - на борту ледокола «Победа». Путешественникам предстоит длительное совместное пребывание, поэтому важно создать благоприятную эмоциональную атмосферу в группе. По результатам проведённого психологического тестирования на совместимость определились пары кандидатов, которым нежелательно находиться в одной группе. Результаты тестирования приведены в таблице (знак «+» на пересечении строки и столбца говорит о том, что данные кандидаты несовместимы).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | + | + | + | |||||
| 2 | + | + | ||||||
| 3 | + | + | + | |||||
| 4 | + | + | + | |||||
| 5 | + | + | ||||||
| 6 | + | + | + | |||||
| 7 | + | + | ||||||
| 8 | + | + |
Разделите кандидатов на две группы для участия в экспедиции: I группа и II группа. Распределение кандидатов начните с условия, что кандидат № 1 находится в I группе. Для каждого кандидата выберите из списка ту группу, в которую он распределён.
Ответ: Кандидат № 1 - I группа, кандидат № 2 - II группа, кандидат № 3 - I группа, кандидат № 4 - II группа, кандидат № 5 - II группа, кандидат № 6 - II группа, кандидат № 7 - I группа, кандидат № 8 - I группа.
Решение задачи:
Построим граф, отображающий совместимость кандидатов: каждому участнику поставим в соответствие вершину графа. Если участники не могут находиться в одной группе - соединим соответствующие вершины ребром:
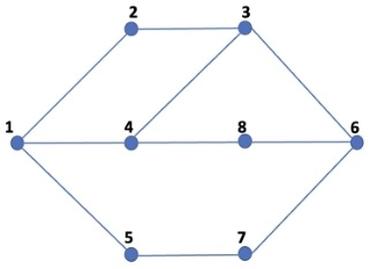
Осуществим поиск в ширину. Пусть вершина 1 будет в I группе, смежные с ней вершины 2, 4, 5 отнесём ко II группе. Вершины, смежные с одной из вершин 2, 4, 5, отнесём к I и так далее, пока не разделим все вершины на две группы. Таким образом, в I группу попадут вершины 1, 3, 8, 7, во II группу - 2, 4, 5, 6.
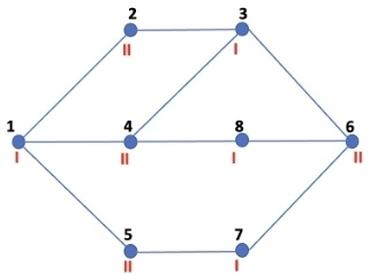
Ответ: I группа - 1387, II группа - 2456.
Задача 7 (Вариант 2)
8 путешественников готовятся к экспедиции на Северный полюс. Участников разделят на две группы, одна из которых будет проводить научные исследования на дрейфующей станции «Север-1», а другая - на борту ледокола «Победа». Путешественникам предстоит длительное совместное пребывание, поэтому важно создать благоприятную эмоциональную атмосферу в группе. По результатам проведённого психологического тестирования на совместимость определились пары кандидатов, которым нежелательно находиться в одной группе. Результаты тестирования приведены в таблице (знак «+» на пересечении строки и столбца говорит о том, что данные кандидаты несовместимы).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | + | + | + | |||||
| 2 | + | + | ||||||
| 3 | + | + | ||||||
| 4 | + | + | + | |||||
| 5 | + | + | + | + | ||||
| 6 | + | + | + | |||||
| 7 | + | + | + | |||||
| 8 | + | + |
Разделите кандидатов на две группы для участия в экспедиции: I группа и II группа. Распределение кандидатов начните с условия, что кандидат № 1 находится в I группе.
Ответ: Кандидат № 1 - I группа, кандидат № 2 - II группа, кандидат № 3 - I группа, кандидат № 4 - I группа, кандидат № 5 - II группа, кандидат № 6 - II группа, кандидат № 7 - I группа, кандидат № 8 - II группа.
Решение задачи:
Построим граф, отображающий совместимость кандидатов: каждому участнику поставим в соответствие вершину графа. Если участники не могут находиться в одной группе - соединим соответствующие вершины ребром:
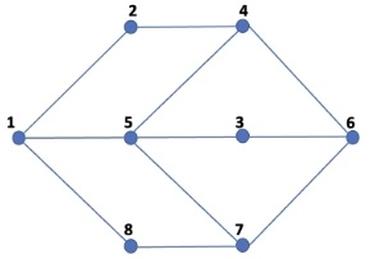
Осуществим поиск в ширину. Пусть вершина 1 будет в I группе, смежные с ней вершины 2, 5, 8 отнесём ко II группе. Вершины, смежные с одной из вершин 2, 5, 8,отнесём к I и так далее, пока не разделим все вершины на две группы. Таким образом, в I группу попадут вершины 1, 4, 3, 7, во II группу - 2, 5, 8, 6.
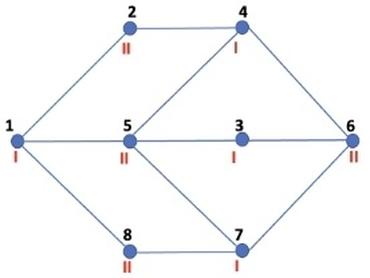
Ответ: I группа - 1437, II группа - 2586.
Задача 8. Агентурные данные.
В современном мире есть много способов записи чисел, дошедших до нас с древних времён. Некоторыми из них мы пользуемся до сих пор (арабской, римской), а другие могут использоваться для кодирования числовой информации.
Агенты мистер и миссис Свит проводили разведывательную операцию и по очереди осуществляли слежку за объектом. Для передачи данных они использовали специальный канал связи, но для большей уверенности применяли дополнительное шифрование сообщений. Например, для записи и передачи числовой информации они каждый день выбирали новую систему счисления.
Во вторник агенты использовали для записи чисел систему счисления, состоящую только из 0 и 1. В этот день мистер Свит сообщил в штаб, что объект совершил 1001 телефонных звонков. В среду миссис Свит определила, что звонков стало больше. Объект звонил чаще, чем во вторник, и количество звонков увеличилось на двоичное число 101. Она записала число выполненных звонков, используя систему счисления, состоящую только из цифр от 0 до 7, и передала в штаб полученные данные.
Какое число отправила миссис Свит в своём сообщении в среду?
Введите число в той системе счисления, в которой велась запись в среду, основания системы счисления записывать не надо.
Ответ: 16
Решение задачи:
10012 + 1012 = 11102 = 1410 = 168
Задание 8 (Вариант 2)
В современном мире есть много способов записи чисел, дошедших до нас с древних времён. Некоторыми из них мы пользуемся до сих пор (арабской, римской), а другие могут использоваться для кодирования числовой информации.
Агенты мистер и миссис Свит проводили разведывательную операцию и по очереди осуществляли слежку за объектом. Для передачи данных они использовали специальный канал связи, но для большей уверенности применяли дополнительное шифрование сообщений. Например, для записи и передачи числовой информации они каждый день выбирали новую систему счисления.
Во вторник агенты использовали для записи чисел систему счисления, состоящую только из 0 и 1. В этот день мистер Свит сообщил в штаб, что объект совершил 1101 телефонных звонков. В среду миссис Свит определила, что звонков стало больше. Объект звонил чаще, чем во вторник, и количество звонков увеличилось на двоичное число 011. Она записала число выполненных звонков, используя систему счисления, состоящую только из цифр от 0 до 7, и передала в штаб полученные данные.
Какое число отправила миссис Свит в своём сообщении в среду?
Введите число в той системе счисления, в которой велась запись в среду, основания системы счисления записывать не надо.
Ответ: 20
Решение задачи:
11012 + 0112 = 100002 = 1610 = 208
Задача 9. Угадай кто?
Коля, Ваня, Антон и Серёжа играли в «Угадай кто?»: ведущий стоит спиной к участникам и должен понять, кто из них дотронулся до его плеча. Серёжа водил уже несколько раз и никак не мог угадать игрока. Тогда друзья решили дать ему подсказку:
Вариант 1
Коля: 1. Это был я. 2. Это был не Антон.
Ваня: 1. Это был Антон. 2. Это был не Коля.
Антон: 1. Это был не я. 2. Это был не Ваня.
Эти подсказки могли запутать Серёжу ещё больше, но он хорошо знал своих друзей и догадался, что один из них оба раза сказал правду; второй оба раза сказал неправду; третий один раз сказал правду, а в другой раз - неправду. Кто из игроков дотронулся до Серёжи?
- Антон
- Коля
- Ваня
- Серёжа
Ответ: Антон
Решение задачи:
Введём следующие обозначения: К - Коля дотронулся до Серёжи, В - Ваня дотронулся до Серёжи, А - Антон дотронулся до Серёжи. Составим таблицу истинности, в которой представим высказывания каждого игрока:
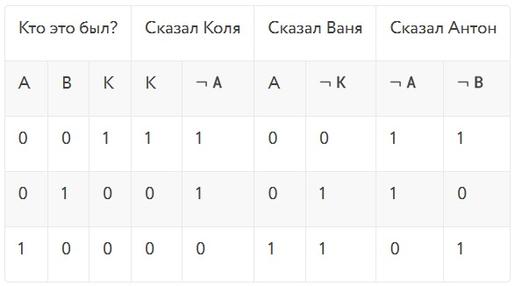
Учитывая догадки Серёжи, найдите строку, где в любом порядке будут три комбинации: 11 (кто-то оба раза сказал правду), 00 (кто-то оба раза сказал неправду), 10 или 01 (кто-то один раз сказал правду, а другой - неправду). В нашей таблице этим условиям удовлетворяет последняя строка. Значит, до плеча Серёжи дотронулся Антон.
Задача 10. Странное устройство.
Во время экологической акции по уборке территории Ваня и Женя обнаружили странный прибор. Он был оснащён двумя кнопками и экраном, на котором светилось число 0. Ваня сразу понял, что первая кнопка увеличивает число на дисплее на 1, а вторая умножает его на 2. В этот момент Женя обнаружил приклеенный на обратной стороне прибора скотчем листок бумаги. Отклеив его, мальчики увидели число 55732248312.
Определите минимальное количество нажатий кнопок на приборе, за которое друзья могут воспроизвести это число на дисплее найденного ими устройства.
Ответ: 58
Решение задачи:
Заметим следующие закономерности:
Если N равно 0, то нажимать на кнопки не требуется. Если N нечётное, уменьшаем его на единицу, потому что предыдущим действием могла быть нажата только первая кнопка. Если N чётное, делим его на 2, поскольку это приведёт к оптимальному решению.
N = 55732248312
k = 2
ans = 0
while N > 0 :
if N % 2 == 0 :
N //= 2
else:
N -= 1
ans += 1
print (ans)